Ultrasound - parameters, wave types, attenuation and reflection

Ultrasound basic parameters

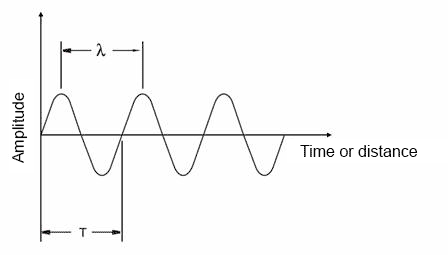
The wave main parameters are wavelength and period. The number of cycles performed in one second is called frequency and is measured in Hertz (Hz). The time it takes to complete a full cycle is called a period and is measured in seconds. The relationship between frequency and period of a wave is given in the formula:

,

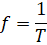• where f – frequency, Hz,
• T – period, s

The speed of sound in an ideal elastic material at a given temperature and pressure is constant. The relationship between ultrasound speed and wavelength is as follows:

,

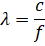• where λ – wavelength, m,
• с – sound speed, m/s

In solids for longitudinal waves, the speed of sound [1]

,

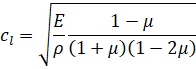• where c_l – speed of sound for longitudinal waves, m/s,
• E – Young's modulus, Pa,
• μ – Poisson's ratio,
• ρ – density, kg/m³

For transverse waves, speed is determined by the formula

,

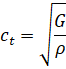• where c_t – sound speed for transverse waves, m/s,
• G – Shear modulus, Pa

Dispersion of sound — the dependence of the phase velocity of monochromatic sound waves on their frequency. The dispersion of the speed of sound can be due to both the physical properties of the medium and the presence of foreign inclusions in it and the presence of the boundaries of the body in which the sound wave propagates.

Types of ultrasonic waves

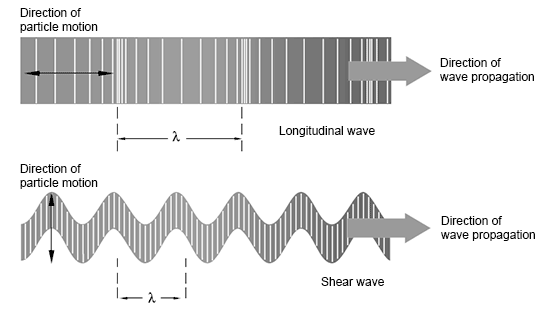
Most ultrasound methods use either longitudinal or shear waves. There are also other forms of sound propagation, including surface waves and Lamb waves.

Longitudinal ultrasonic waves - waves, the direction of propagation of which coincides with the direction of displacement and velocities of the particles of the medium.

Transverse ultrasonic waves - waves propagating in a direction perpendicular to the plane in which the directions of displacements and velocities of body particles lie, the same as shear waves [2].

Surface (Rayleigh) ultrasonic waves have an elliptical motion of particles and propagate over the surface of the material. Their speed is approximately 90% of the shear wave propagation speed, and their penetration deep into the material is equal to approximately one wavelength [3].

Lamb wave is an elastic wave propagating in a solid plate (layer) with free boundaries, in which the vibrational displacement of particles occurs both in the direction of wave propagation and perpendicular to the plane of the plate. Lamb waves are one of the types of normal waves in an elastic waveguide - in a plate with free boundaries. The pattern of motion in them and their properties are more complex than those of waves in unbounded solids, because these waves must satisfy not only the equations of the theory of elasticity, but also the boundary conditions on the surface of the plate.

Visualization of ultrasonic waves

Ultrasound intensity and power

Sound intensity is the time-average energy carried by a sound wave through a unit area perpendicular to the direction of wave propagation, per unit time. For periodic sound, averaging is performed either over a period of time larger than the period or over an integer number of periods [2]. Ultrasound intensity is a value that expresses the power of the acoustic field at a point [6].

For a sinusoidal traveling plane wave, the ultrasound intensity I is determined by the formula

,

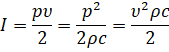• где р — sound pressure amplitude, Pa
• v — particles vibration velocity amplitude, m/s
• ρ — density, kg/m³
• с — sound speed, m/s

In a spherical traveling wave, the ultrasound intensity is inversely proportional to the square of the distance from the source. In a standing wave, I = 0, that is, there is, on average, no sound energy flow. The intensity of ultrasound in a harmonic plane traveling wave is equal to the energy density of the sound wave multiplied by the speed of sound. The flow of sound energy is characterized by the so-called Umov vector - the vector of the energy flux density of the sound wave, which can be represented as the product of the ultrasound intensity by the wave normal vector, i.e., a unit vector perpendicular to the wavefront. If the sound field is a superposition of harmonic waves of different frequencies, then the additivity of the components takes place for the vector of the average density of the sound energy flux.

For emitters that create a plane wave, speak of the radiation intensity, meaning by this the specific power of the emitter, that is, the emitted sound power per unit area of the emitting surface.

Sound intensity is measured in SI units in W/m². In ultrasound technology, the range of changes in the intensity of ultrasound is very large - from threshold values of ~ 10^-12 W/m² to hundreds of kW/m² at the focus of ultrasonic concentrators.

Sound power is the energy transmitted by a sound wave through the considered surface per unit of time. Distinguish between the instantaneous value of the ultrasound power and the average over a period or over a long time. Of greatest interest is the average value of the ultrasound power per unit area, the so-called average specific sound power, or sound intensity [2].

Table 1 - Properties of some common materials [6]

Material	Density, kg/m3	Longitudinal wave speed, m/s	Transverse wave speed, m/s	Acoustic impedance, 103 kg/(м2*s)
Acrylic	1180	2670	-	3,15
Air	0,1	330	-	0,00033
Aluminum	2700	6320	3130	17,064
Brass	8100	4430	2120	35,883
Copper	8900	4700	2260	41,830
Glass	3600	4260	2560	15,336
Nickel	8800	5630	2960	49,544
Polyamide (nylon)	1100	2620	1080	2,882
Steel (low alloy)	7850	5940	3250	46,629
Titanium	4540	6230	3180	26,284
Tungsten	19100	5460	2620	104,286
Water (293К)	1000	1480	-	1,480

Ultrasound attenuation

One of the main characteristics of ultrasound is its attenuation. Attenuation of ultrasound is the decrease in the amplitude and, therefore, the intensity of the sound wave as it propagates. The attenuation of ultrasound occurs for a number of reasons. The main ones are:

• decrease in wave amplitude with distance from the source, due to the shape and wave dimensions of the source;
• scattering of ultrasound by inhomogeneities of the medium, as a result of which the energy flux in the initial direction of propagation decreases;
• absorption of ultrasound, i.e. irreversible transfer of the energy of a sound wave into other forms, in particular into heat.

The first of these reasons is associated with the fact that as the wave propagates from a point or spherical source, the energy emitted by the source is distributed over the increasing surface of the wavefront and, accordingly, the energy flux through the unit surface decreases, i.e. sound intensity. For a spherical wave, the wave surface of which grows with a distance r from the source as r², the wave amplitude decreases proportionally to r ^-1, and for a cylindrical wave - proportionally to r ^-1/2.

The scattering of ultrasound occurs due to a sharp change in the properties of the medium - its density and elastic moduli - at the boundary of inhomogeneities, the dimensions of which are comparable to the wavelength. In gases, it can be, for example, liquid drops, in an aqueous medium - air bubbles, in solids - various foreign inclusions or individual crystallites in polycrystals, etc. Scattering by inhomogeneities chaotically distributed in space is of particular interest.

The absorption of ultrasound can be due to various mechanisms. An important role is played by the viscosity and thermal conductivity of the medium, the interaction of the wave with various molecular processes of the substance, with thermal vibrations of the crystal lattice, etc.

The sound attenuation due to scattering and absorption is described by an exponential law of decreasing amplitude with distance, i.e., the amplitude is proportional to e^-δr, and the intensity is proportional to e^-2δr, in contrast to the power law of decreasing amplitude when the wave diverges, where δ is the sound attenuation coefficient[2].

The attenuation coefficient is expressed either in decibels per meter (dB/m) or in nepers per meter (Np/m).

For a plane wave, the attenuation coefficient by amplitude with distance is determined by the formula [4]

,

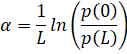• where α – attenuation coefficient with distance, 1/m or Np/m,
• L – distance, m,
• p(0), p(L) – sound pressure amplitude at the initial point and at a distance L, Pa

Reciprocal time constant (the attenuation coefficient versus time) is determined [5]

,

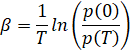• where β – reciprocal time constant, 1/s or Np/s,
• T – time, s,
• p(0), p(T) – the amplitude of sound pressure at the beginning and after time T, respectively, Pa

To measure the coefficient, the unit dB/m is also used, in this case

,

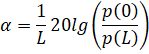Decibel (dB) is a logarithmic unit of measurement of the ratio of energies or powers in acoustics [2].

,

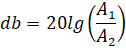• where A₁ – first signal amplitude,
• A₂ – second signal amplitude

Then the relationship between the units of measurement (dB/m) and (1/m) will be:

,

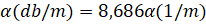The attenuation coefficient is expressed in either decibels per meter (dB/m), or nepers per meter (Np/m) or equivalently m^-1. Attenuation of 1 Np/m means that at a distance of 1 m the wave amplitude decreases by a factor of e (e = 2.71 is the base of natural logarithms or Euler's number).

1 Np/m = 8,68 dB/m

Reflection of ultrasound from the interface

When a sound wave strikes the medium interface, part of the energy will be reflected in the first medium, and the rest of the energy will pass into the second medium. The ratio between the reflected energy and the energy passing into the second medium is determined by the acoustic impedance of the first and second medium. In the absence of sound speed dispersion, the acoustic impedance does not depend on the waveform and is expressed by the formula:

,

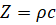• where Z – acoustic impedance, kg/(m²s),
• ρ – density, kg/m³,
• с – sound speed, m/s

The reflection and transmission coefficients will be determined as follows

,

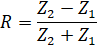• where R – sound pressure reflection coefficient [1],
• Z₁ – the acoustic impedance of the first substance in which a sound wave propagates, kg/(m²s),
• Z₂ – the acoustic impedance of the second substance into which the sound wave passes, kg/(m²s)

,

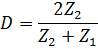• where D – sound pressure transmission coefficient

It should also be noted that if the second medium is acoustically softer, i.e. Z₁>Z₂, then at the reflection the phase of the wave changes by 180˚ [1].

The energy transmission coefficient τ from one medium to another is determined by the ratio of the wave intensity passing into the second medium to the intensity of the incident wave

,

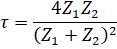Interference and diffraction of ultrasonic waves

Interference of sound — the unevenness of the spatial distribution of the amplitude of the resulting sound wave, depending on the relationship between the phases of the waves, added at one point or another in space. When harmonic waves of the same frequency are added, the resulting spatial distribution of amplitudes forms a time-independent interference pattern, which corresponds to the change in the phase difference of the constituent waves when passing from point to point. For two interfering waves, this pattern on the plane has the form of alternating bands of amplification and attenuation of the amplitude of the quantity characterizing the sound field (for example, sound pressure). For two plane waves, the stripes are rectilinear with an amplitude that varies across the stripes according to a change in the phase difference. An important special case of interference is the addition of a plane wave with its reflection from a plane boundary; in this case, a standing wave is formed with the planes of nodes and antinodes located parallel to the boundary.

Sound diffraction is the deviation of the sound behavior from geometric acoustics, due to the wave nature of sound. The result of sound diffraction is the divergence of ultrasonic beams when moving away from the emitter or after passing through a hole in the screen, bending of sound waves into the shadow region behind obstacles that are large compared to the wavelength, the absence of a shadow behind obstacles that are small compared to the wavelength, etc. Sound fields created by diffraction of the initial wave by obstacles placed in the medium, by inhomogeneities of the medium itself, as well as by irregularities and inhomogeneities of the boundaries of the medium, are called scattered fields.

Ultrasound emitters

Ultrasound emitters are devices used to excite ultrasonic vibrations and waves in gaseous, liquid, and solid media. Ultrasound emitters convert energy of some other kind to the energy of the sound field.

The most widely used ultrasound emitters are electro-acoustic transducers. In the overwhelming majority of ultrasound emitters of this type, namely in piezoelectric transducers, magnetostrictive transducers, electrodynamic emitters, electromagnetic and electrostatic emitters, electrical energy is converted into vibration energy of some solid body (emitting plate, rod, diaphragm, etc.), which emits acoustic waves into the environment. All of these transducers are, as a rule, linear, and, therefore, the oscillations of the radiating system reproduce in shape the exciting electrical signal; only at very high amplitudes of oscillations near the upper limit of the dynamic range of the ultrasound emitter can nonlinear distortions occur.

In a transducer designed to emit a monochromatic wave, the phenomenon of resonance is used: they operate on one of the natural oscillations of a mechanical oscillatory system, to the frequency of which the oscillator that excites the transducer is tuned. Electroacoustic transducers that do not have a solid-state emitting system are used relatively rarely as ultrasound emitters; these include, for example, ultrasound emitters based on an electric discharge in a liquid or on electrostriction of a liquid [2].

Ultrasound transducer characteristics

The main characteristics of ultrasound emitters are their frequency spectrum, emitted sound power, radiation directivity. In the case of mono frequency radiation, the main characteristics are the operating frequency of the ultrasound emitter and its frequency band, the boundaries of which are determined by the decrease in the radiated power by half in comparison with its value at the frequency of maximum radiation. For resonant electroacoustic transducers, the operating frequency is the natural frequency f₀ of the transducer, and the bandwidth Δf is determined by its quality factor Q.

,

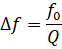Ultrasound emitters (electroacoustic transducers) are characterized by sensitivity, electroacoustic efficiency, and their own electrical impedance.

The sensitivity of an ultrasound emitter is the ratio of the sound pressure at the maximum of the directivity characteristic at a certain distance from the emitter (most often at a distance of 1 m) to the electric voltage on it or to the current flowing in it. This characteristic applies to ultrasound emitters used in audible alarms, sonar, and other similar devices. For emitters of technological purposes, used, for example, in ultrasonic cleaning, coagulation, exposure on chemical processes, the main parameter is power. Along with the total radiated power, estimated in W, ultrasound emitters are characterized by the specific power (surface power density), i.e. the average power per unit area of the radiating surface, or the average radiation intensity in the near field, estimated in W/m².

The efficiency of electroacoustic transducers emitting acoustic energy into the sounding medium is characterized by the value of their electroacoustic efficiency, which is the ratio of the emitted acoustic power to the consumed electrical power. In acoustoelectronics, to assess the efficiency of ultrasound emitters, the so-called electrical loss factor is used, which is equal to the ratio (in dB) of electrical power to acoustic power. The efficiency of ultrasonic tools used in ultrasonic welding, machining, and the like is characterized by the so-called efficiency ratio, which is the ratio of the square of the amplitude of the vibrational displacement at the working end of the concentrator to the electrical power consumed by the transducer. Sometimes the effective electromechanical coupling coefficient is used to characterize the energy conversion in ultrasound emitters.

Emitter sound field

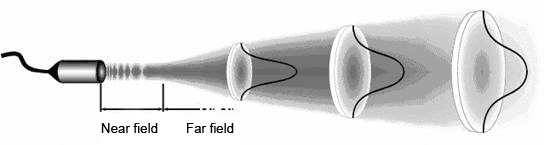
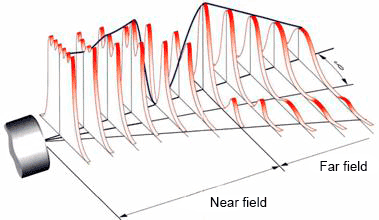
The sound field of the transducer is divided into two zones: the near zone and the far zone. The near zone is the area directly in front of the transducer where the echo amplitude passes through a series of highs and lows. The near zone ends at the last maximum, which is located at a distance N from the transducer. It is known that the location of the last maximum is the natural focus of the transducer. The far zone is the area behind N where the sound field pressure gradually decreases to zero [1].

The position of the last maximum N on the acoustic axis, in turn, depends on the diameter and wavelength, and for a disk circular radiator is expressed by the formula

,

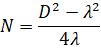• where N – near field length, m,
• D – emitter diameter, m,
• λ – wavelength, m

However, since D is usually much larger than λ, the equation can be simplified and reduced to the form

,

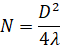The characteristics of the sound field are determined by the design of the ultrasonic transducer.

Ultrasound application

The various applications of ultrasound, in which its various features are used, can be conditionally divided into three directions. The first is associated with the receipt of information by means of ultrasonic waves, the second - with an active effect on the substance, and the third - with the processing and transmission of signals (directions are listed in the order of their historical formation). For each specific application, ultrasound of a certain frequency range is used.

Obtaining information using ultrasound methods. Ultrasonic methods are widely used in scientific research to study the properties and structure of substances, to clarify the processes taking place in them at the macro and micro levels. These methods are based mainly on the dependence of the speed of propagation and attenuation of acoustic waves on the properties of substances and on the processes occurring in them.

The effect of ultrasound on a substance. The active effect of ultrasound on a substance, leading to irreversible changes in it, or the effect of ultrasound on physical processes, affecting their course, is due in most cases to nonlinear effects in the sound field. This effect is widely used in industrial technology; in this case, the problems solved with the help of ultrasonic technology, as well as the mechanism of ultrasonic action itself, are different for different media.

Signal processing and transmission. Ultrasonic devices are used for the conversion and analog processing of electrical signals in various branches of radio electronics, for example, in radar, communications, computing, and for controlling light signals in optics and optoelectronics. In devices for controlling electrical signals, the following features of ultrasound are used: low propagation velocity in comparison with electromagnetic waves; low absorption in crystals and, accordingly, high Q-factor of resonators [2].